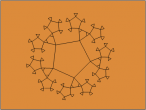
Dodecahedron

Dodecahedron is one of the five Platonic Solids. It consists of

• 12 faces (congruent pentagons)
• 30 edges
• 20 vertices (the meeting of 3 faces)

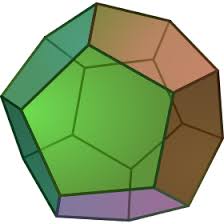
Construction

From Trigonometry

A basic pentagon can be created from the basic code

; 
REPEAT 5 [ FD 2 RT 72]

note: the internal angle of a regular pentagon is 108^o, making the external angle, which we are are turning, 72^o

from this initial pentagon, we need to create pentagons connecting to our 5 initial edges. To do this, we need to consider what angle these are to be connected at. The dihedral angle of a dodecahedron is116.56505° = arccos(-1/√5), meaning that we need to tilt down 63.43495^o

this process needs to be repeated several times to create all edges of our dodecahedron. The final code would look something like.

REPEAT 3 [
REPEAT 1 [FD 2 RT 72] TL 63.43495
REPEAT 5 [FD 2 LT 72]
TR 63.43495
REPEAT 1 [FD 2 RT 72] TL 63.43495
REPEAT 4 [FD 2 LT 72] LT 108 TL 63.43495
REPEAT 5 [FD 2 LT 72] TR 63.43495
RT 108 FD 2 LT 72 TR 63.43495
REPEAT 3 [FD 2 RT 72]
RT 108 TR 63.43495]